Формула расчета передаточного числа

Формула расчета передаточного числа

Как рассчитать передаточное отношение шестерен механической передачи.

В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев. Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев.

Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.

Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.

Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.

Итак, рассмотрим пример расчета с использованием двух шестерен.

Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.

В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.

Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.

Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.

Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.

Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.

Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.

В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.

Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.

Определим теперь частоту вращения.

Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.

Будем использовать формулу: S1 × T1 = S2 × T2,

S1 – частота вращения желтой (ведущей) шестерни,

Т1 – количество зубьев желтой (ведущей) шестерни;

S2- частота вращения красной шестерни,

Т2 – количество зубьев красной шестерни.

В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.

340 rpm × 7 = S2 × 40

Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.

Расчёт передаточного числа

В каждой передаче элемент который передаёт мощность, называется ведущим, а элемент которому подается эта мощность ведомым. Чаще всего число оборотов ведущего элемента n₁ и ведомого элемента n₂ различно. Отношение этих чисел оборотов называется передаточным числом.

(7)

Передачи могут быть понижающие ί>1; n₁>n₁ и повышающие, если ί

(8)

ξ – относительное скольжение зависят от материала фрикционных дисков и составляет 0,002-0,03;

ί – у фрикционных передач чепце всего составляет 5-7;

ί – у плоскоременных передач до 10, клиноременных до 15.

Для зубчатой передачи:

(9)

z_k – число зубьев колеса

z_ш – число зубьев шестерни

ί – для цилиндрических прямозубых колёс до 10 , для конических до 5, для червячных до 80

Для червячной передачи:

(10)

Z_r – число заходов червяка

Z_k – число зубьев колеса

ί –для червячных до 80

Для цепной передачи:

(11)

Z₂ – количество зубьев ведомой звездочки;

Z₁ – количество зубьев ведущей звездочки;

D_1, D₂ – соответственно диаметры делительной окружности звёздочек

ί – обычно ≤8, в тихоходных достигает 15.

Контрольные вопросы по теме:

Фрикционные передачи

1. Из каких элементов состоит фрикционная передача?

2. Что такое пробуксовывание и когда оно возникает?

3. Достоинства и недостатки фрикционных передач.

4. Область применения фрикционных передач.

5. Как определяется передаточное число фрикционных передач?

6. Назовите основные требования, предъявляемые к материалу фрикционных передач.

7. Назовите разновидности бесступенчатых передач.

8. От чего зависит форма тел качения фрикционных передач?

9. Назовите современные тенденции развития фрикционных вариаторов.

10. Достоинства и недостатки фрикционных передач, работающих в масле и без смазочного материала.

Ременные передачи

1. Из каких элементов состоит ременная передача?

2. Достоинства и недостатки ременных передач.

3. Где получили наибольшее распространение ременные передачи?

5. Как классифицируются ременные передачи по форме сечения ремня?

6. Как классифицируются ремни в ременных передачах?

7. Из чего состоят хлопчатобумажные ремни?

8. Чем пропитывают шерстяные тканые ремни?

9. Достоинства бесконечных ремней.

10. Основные типы конструкций клиновых ремней.

11. Что такое корд ткань?

13. Из какого материала выполняют корд?

14. Основные виды зубчатых ремней.

15. Как определяется передаточное число в ременных передачах?

Цепные передачи

1. Из чего состоит цепная передача?

2. Достоинства и недостатки цепных передач.

3. Где получили наибольшее распространение цепные передачи?

4. Какие виды цепей используют в цепных передачах?

5. Сравните конструкции втулочной и втулочно-роликовой цепей.

6. Объясните конструкцию зубчатой цепи.

7. Какие существуют условия изготовления звездочек?

8. Какие материалы используют для изготовления звездочек?

9. Как определяется передаточное число в цепных передачах?

Зубчатые передачи

1. Почему зубчатые передачи получили широкое распространение?

2. Что представляют собой зубчатые передачи?

3. Из чего состоят зубчатые передачи?

4. Какие формы поверхностей используют для нарезки зубьев?

5. Классификация валов по взаимному расположению.

7. Классификация валов по относительному характеру движения.

8. Какую систему используют для преобразования вращательного движения в поступательное?

10. Чем определяется свойства зацепления?

11. Какие виды зацепления вы знаете?

12. Достоинства и недостатки косозубых зубчатых колёс.

13. Достоинства зубчатых передач.

14. Недостатки зубчатых передач.

15. Какое колесо называется шестерней?

16. Как определяется передаточное число?

17. Какие зубчатые передачи передают движение в другую плоскость?

Расчет максимальной скорости автомобиля

Привет друзья! Более года ничего не писал в свой блог, но сегодня что-то пошло не так . Не туда забрел, не там почитал, и пришло вдохновение, желание двигаться вперед.

Это будет не информационный пост как обычно, а некий мануал, калькулятор, который в зависимости от заданных типоразмеров шин, оборотов мотора и указанных передаточных чисел коробки рассчитает, какая будет скорость движения у автомобиля на передачи.

Конечно, калькулятор скорости автомобиля по передаточным числам и шинам производит расчет в идеальных (лабораторных) условиях. В реальных же условиях на конечную скорость автомобиля влияет очень много факторов, начиная от климатических условий и состояния дорожного полотна, и заканчивая настройкой мотора. Другими словами, калькулятор показывает потенциал коробки передач, до какой максимальной скорости она способна разогнать автомобиль.

Калькулятор расчет максимальной скорости автомобиля и КПП

Прогноз максимальной скорости движения авто на передаче:

* Для сликов маркированных в дюймах вводите только R колеса (вводить ширину и профиль не надо).

По умолчанию в калькуляторе расчета передаточных чисел КПП указаны характеристики коробок S4C (КПП #1) и S9B (КПП #2). Выбрал эти коробки не случайно, т.к. первая устанавливалась на Civic EK9, а вторая считается самой длинной МКПП для Б-моторов.

Размеры шин, количество оборотов двигателя, передаточные числа КПП и главную пару Вы можете подставлять на свое усмотрение. Калькулятором представляет собой универсальное средство, поэтому не стоит зацикливаться, что он работает только на КПП предназначенных для Хонды. Коробку ВАЗ’ика он тоже рассчитает без проблем

Внимание ! Калькулятор КПП и максимальной скорости движения автомобиля предоставлен исключительно в ознакомительных целях и не гарантирует 100% достоверных данных!

На форуме есть несколько тем, посвященных Honda коробкам, из которых Вы можете узнать передаточные числа для калькулятора. Информация еще не полная, но со временем, усилиями сообщества обновим топики и сделаем полную подборку характеристик:

– КПП и передаточные числа для моторов B серии;
– КПП и передаточные числа для моторов K серии;
– КПП и передаточные числа для моторов H серии;
– КПП и передаточные числа для моторов F серии.
–

В завершении поста, хочу заметить, что при установке на автомобиль дисков большего диаметра или шин отличных от стокового типоразмера, спидометр будет выдавать не совсем корректные данные. Единицы отдают его на калибровку, чтобы снимать точные показания, в 99.999% случаев автовладельцы оставляют все как есть. Чтобы узнать, насколько спидометр “обманывает” Вас, в блоге есть еще один полезный инструмент:

Спасибо за внимание и отдельный респект всем тем, кто поделился ссылкой на пост

P.S. По давней традиции, не забывайте подписываться на обновления проекта и нашего паблика ВКонтакте, рассказывать друзьям о проекте, делиться в сети ссылками на интересные посты, оставлять развернутые комментарии по теме, делать ретвиты, ставить лайки, нажимать на “мне нравится”, добавлять посты в гугл плюс и . И конечно же, САМОЕ-САМОЕ ГЛАВНОЕ – приглашаю всех на форум любителей хонда . С момента последнего поста много чего изменилось и форум тоже. Жду всех на форуме

8.4: Передаточное отношение

Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза. В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.

Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.

Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.

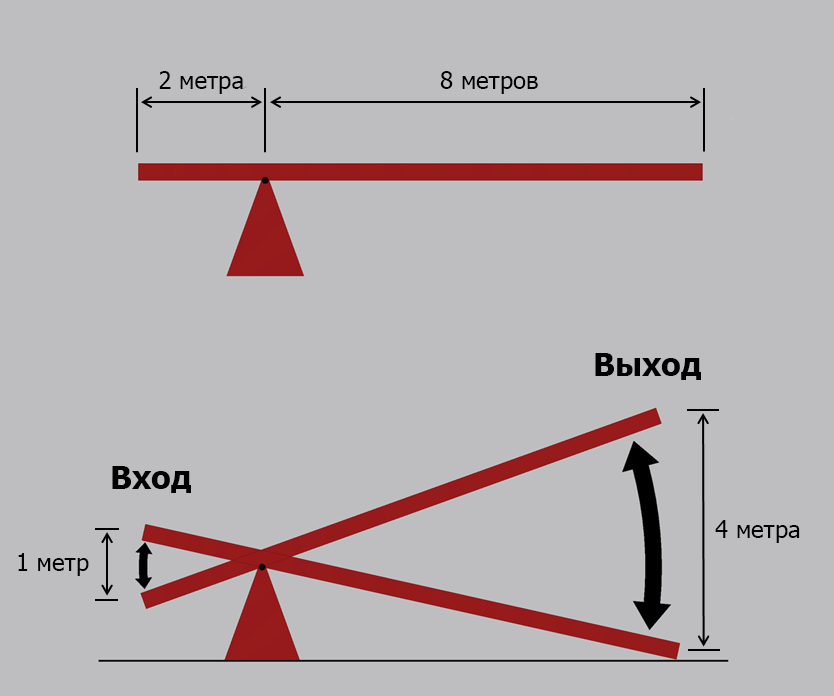
В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.

Длина на выходе / Длина на входе = 8 / 2 = 4

Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.

В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?

Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:

Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м

Далее, необходимо рассчитать равнодействующую силу на выходе:

Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон

Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!

Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.

Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.

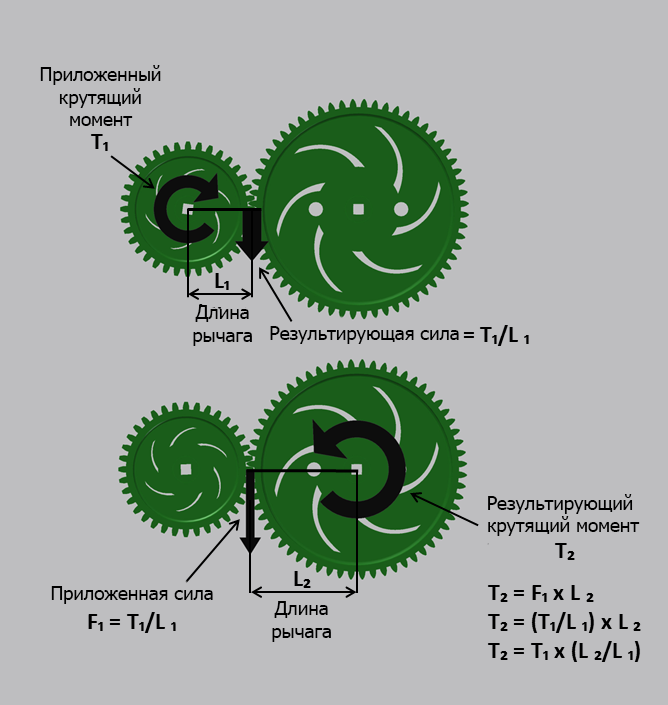
Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.

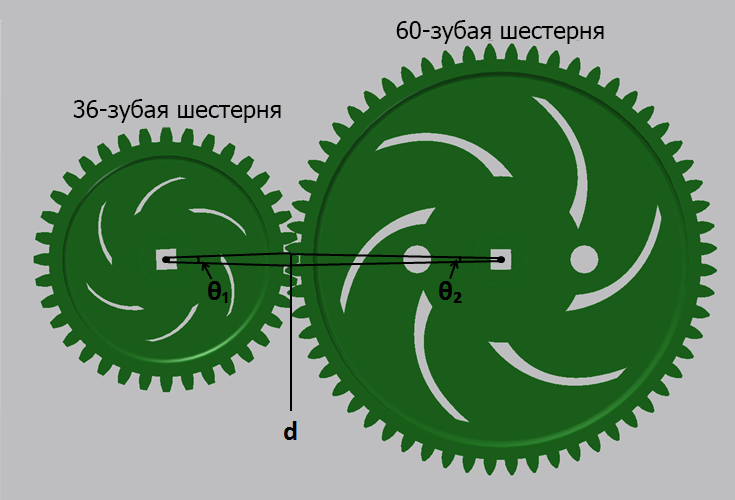
В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).

Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.

Из примеров 8.1 – 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними. Это называется передаточным числом.

Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.

Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67

Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5

Глядя на пример, представленный выше.

Предельный перегрузочный момент второго вала может быть рассчитан по формуле:

Выходной момент = Входной момент х Передаточное число

Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м

Свободная скорость второго вала может быть рассчитана по формуле:

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин

Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.

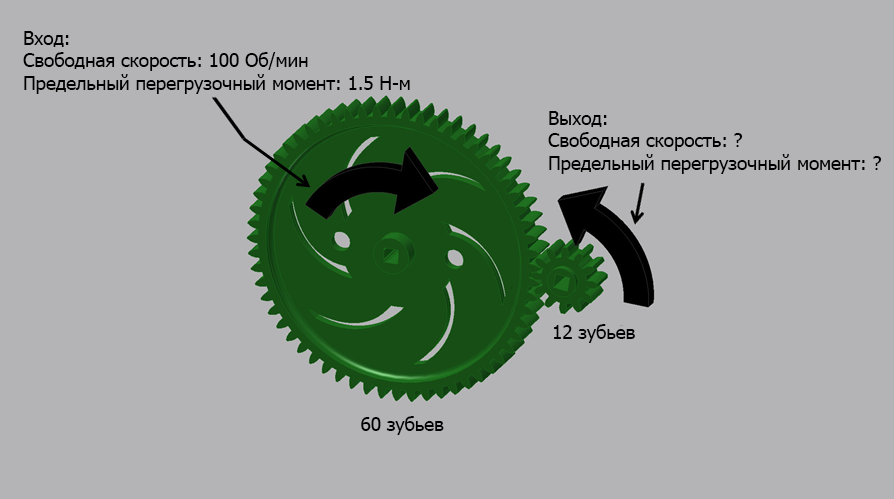
Для второго примера расчеты могут быть произведены тем же способом.

Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2

Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин

Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.

Выбор мотор-редуктора

В данной статье содержится подробная информация о выборе и расчете мотор-редуктора. Надеемся, предлагаемые сведения будут вам полезны.

При выборе конкретной модели мотор-редуктора учитываются следующие технические характеристики:

• тип редуктора;
• мощность;
• обороты на выходе;
• передаточное число редуктора;
• конструкция входного и выходного валов;
• тип монтажа;
• дополнительные функции.

Тип редуктора

Наличие кинематической схемы привода упростит выбор типа редуктора. Конструктивно редукторы подразделяются на следующие виды:

Червячный одноступенчатый со скрещенным расположением входного/выходного вала (угол 90 градусов).

Червячный двухступенчатый с перпендикулярным или параллельным расположением осей входного/выходного вала. Соответственно, оси могут располагаться в разных горизонтальных и вертикальных плоскостях.

Цилиндрический горизонтальный с параллельным расположением входного/выходного валов. Оси находятся в одной горизонтальной плоскости.

Цилиндрический соосный под любым углом. Оси валов располагаются в одной плоскости.

В коническо-цилиндрическом редукторе оси входного/выходного валов пересекаются под углом 90 градусов.

ВАЖНО!
Расположение выходного вала в пространстве имеет определяющее значение для ряда промышленных применений.

• Конструкция червячных редукторов позволяет использовать их при любом положении выходного вала.
• Применение цилиндрических и конических моделей чаще возможно в горизонтальной плоскости. При одинаковых с червячными редукторами массо-габаритных характеристиках эксплуатация цилиндрических агрегатов экономически целесообразней за счет увеличения передаваемой нагрузки в 1,5-2 раза и высокого КПД.

Таблица 1. Классификация редукторов по числу ступеней и типу передачи

Передаточное число [I]

Передаточное число редуктора рассчитывается по формуле:

I = N1/N2

где
N1 – скорость вращения вала (количество об/мин) на входе;
N2 – скорость вращения вала (количество об/мин) на выходе.

Полученное при расчетах значение округляется до значения, указанного в технических характеристиках конкретного типа редукторов.

Таблица 2. Диапазон передаточных чисел для разных типов редукторов

ВАЖНО!
Скорость вращения вала электродвигателя и, соответственно, входного вала редуктора не может превышать 1500 об/мин. Правило действует для любых типов редукторов, кроме цилиндрических соосных со скоростью вращения до 3000 об/мин. Этот технический параметр производители указывают в сводных характеристиках электрических двигателей.

Крутящий момент редуктора

Крутящий момент на выходном валу [M2] – вращающий момент на выходном валу. Учитывается номинальная мощность [Pn], коэффициент безопасности [S], расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.

Номинальный крутящий момент [Mn2] – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.

Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.

Необходимый крутящий момент [Mr2] – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.

Расчетный крутящий момент [Mc2] – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:

Mc2 = Mr2 x Sf ≤ Mn2

где
Mr2 – необходимый крутящий момент;
Sf – сервис-фактор (эксплуатационный коэффициент);
Mn2 – номинальный крутящий момент.

Эксплуатационный коэффициент (сервис-фактор)

Сервис-фактор (Sf) рассчитывается экспериментальным методом. В расчет принимаются тип нагрузки, суточная продолжительность работы, количество пусков/остановок за час эксплуатации мотор-редуктора. Определить эксплуатационный коэффициент можно, используя данные таблицы 3.

Таблица 3. Параметры для расчета эксплуатационного коэффициента

Нельзя делать расчеты, используя приблизительное значение входной мощности, так как КПД могут существенно отличаться.

Коэффициент полезного действия (КПД)

Расчет КПД рассмотрим на примере червячного редуктора. Он будет равен отношению механической выходной мощности и входной мощности:

где
P2 – выходная мощность;
P1 – входная мощность.

ВАЖНО!
В червячных редукторах P2

Источники:

http://konvenat.ru/categories/technology/192-gearscalc
http://megaobuchalka.ru/3/29639.html
http://www.mytyper.ru/manuals/calculation-of-the-maximum-speed-of-the-car/
http://vex.examen-technolab.ru/lessons/unit_8_mechanical_power_transmission/82/
http://tehprivod.su/poleznaya-informatsiya/kak-vybrat-motor-reduktor.html