Через что на колесо передается вращательное движение

Механизмы передачи движения, применяемые в токарных станках.

Передача вращательного движения.

• Ременная передача– система состоит из двух шкифов, ведущего и ведомого, и соединяющего их ремня. Движение ведущего шкифа передается на ремень, ремень передает его ведомому шкифу.

Ременные передачи могут быть плоскими и клиноременными, позволяют соединять валы, расположенные на значительном расстоянии друг от друга.

Движение передается за счет сил трения.

Передаточное отношение = D1/D2

• Зубчатая передача –вращательное движение передается через зацепления зубчатых колес.

Характеристики зубчатых колес:

Модуль (m) – это часть диаметра делительной окружности, приходящаяся на один зуб.

Диаметр делительной окружности d = mZ.

Число зубьев – Z.

В каждом зубчатом колесе различают три окружности: делительную окружность, окружность выступов, окружность впадин и три соответствующих им диаметра.

Делительная окружность – условная, делит зуб на две неравные части: головку зуба и ножку зуба.

Шаг (Р) – это расстояние между одноименными точками двух соседних зубьев, измеренные по дуге делительной окружности.

Передаточное отношение =Z1/Z2,

где Z1- число зубьев ведущего зубчатого колеса, Z2 – число зубьев ведомого зубчатого колеса.

Основное условие – равенство окружных шагов ведущего и ведомого колес.

• Червячная передача – это зубчато-винтовая передача, которая состоит из винта с трапецеидальной резьбой – червяка и червячного колеса.

По сравнению с другими передачами обеспечивает плавность и бесшумность работы, но в тоже время происходит большая потеря мощности на трение.

Передаточное отношение = Z1/Z2, где – Z1 – число заходов червяка, Z2 – число зубьев червячного колеса.

Преобразование вращательного движения в поступательное.

• Винтовая передача– состоит из винта и гайки.

а) передача с вращающимся винтом и ведомой, поступательно перемещающейся гайкой

б) передача с вращающимся и одновременно поступательно перемещающимся винтом при неподвижной гайке.

в) передача с вращающейся гайкой и ведомым поступательно перемещающимся винтом.

За один оборот линейное перемещение гайки = произведению шага винта на число заходов винта= ход резьбы.

• Зубчато-реечный механизм – состоит из зубчатой рейки и зубчатого колеса.

При вращении колеса рейка перемещается.

Величина поступательного перемещения рейки = πmZn, где m – модуль, Z – число зубьев колеса, n – частота вращения колеса, π = 3,14.

Вращательное движение тела. Закон вращательного движения

В этой статье описывается важный раздел физики – “Кинематика и динамика вращательного движения”.

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела – это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

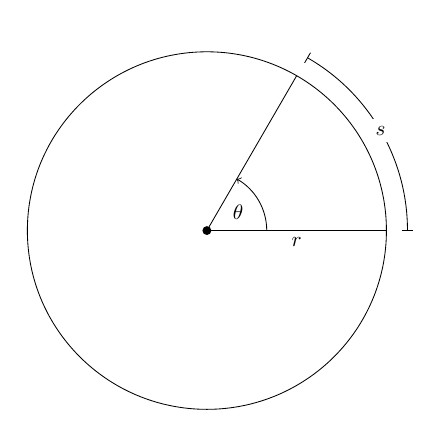
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

Если φ измерять в радианах (1 рад – это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

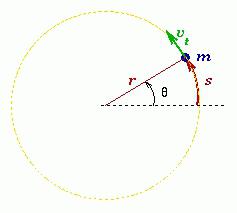
Угловая скорость материальной точки или тела – это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

Согласно предварительной формуле размерность угловой скорости

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T – физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

поэтому период вращения определим следующим образом:

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

Единицы измерения частоты: [ν]= 1/c = 1 c -1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено – dω/dt 2 /r = ω 2 r 2 /r.

Итак, в скалярном виде

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

Момент импульса материальной точки

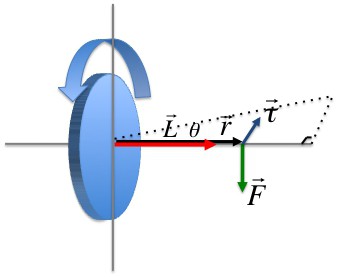
Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_i к υ_i правый винт покажет направление вектора L_i).

В скалярной форме

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

Так что момент импульса материальной точки для вращательного движения примет вид

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

Если вместо линейной скорости подставить ее выражение через угловую:

то выражение для момента импульса примет вид

Величина I_i = m_ir_i 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

Момент силы и момент инерции

Закон вращательного движения гласит:

Известно, что представить момент импульса тела можно через момент инерции:

Учитывая, что угловое ускорение определяется выражением

получим формулу для момента силы, представленного через момент инерции:

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I + ma 2 ,

где I – начальный момент инерции тела; m – масса тела; a – расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Через что на колесо передается вращательное движение

Механическая энергия, используемая для приведения в движение машины-орудия, представляет собой энергию вращательного движения вала двигателя. Вращательное движение получило наибольшее распространение в механизмах и машинах, так как обладает следующими достоинствами: обеспечивает непрерывное и равномерное движение при небольших потерях на трение; позволяет иметь простую и компактную конструкцию передаточного механизма.

Все современные двигатели для уменьшения габаритов и стоимости выполняют быстроходными с весьма узким диапазоном изменения угловых скоростей. Непосредственно быстроходный вал двигателя соединяют с валом машины редко (вентиляторы и т. п.). В абсолютном большинстве случаев режим работы машины-орудия не совпадает с режимом работы двигателя, поэтому передача механической энергии от двигателя к рабочему органу машины осуществляется с помощью различных передач.

Передачей будем называть устройство, предназначенное для передачи энергии из одной точки пространства в другую, расположенную на некотором расстоянии от первой.

В современном машиностроении в зависимости от вида передаваемой энергии применяют механические, пневматические, гидравлические и электрические передачи. В курсе «Детали машин» рассматривают только наиболее распространенные механические передачи.

Механическими передачами, или просто передачами, называют механизмы для передачи энергии от машины-двигателя к машине-орудию, как правило, с преобразованием скоростей, моментов, а иногда — с преобразованием видов (например, вращательное в поступательное) и законов движения.

Передача (в механике) соединяет вал источника энергии – двигателя и валы потребителей энергии – рабочих органов машины, таких, например, как ведущие колёса гусеничного движителя или автомобиля.

Механические передачи известны со времен зарождения техники, прошли вместе с ней длительный путь развития и совершенствования и имеют сейчас очень широкое распространение. Грамотная эксплуатация механических передач требует знания основ и особенностей их проектирования и методов расчетов.

При проектировании к механическим передачам предъявляются следующие требования:

– высокие нагрузочные способности при ограниченных габаритных размерах, весе, стоимости;

– постоянство передаточного отношения или закона его изменения;

– обеспечение определенного взаимного расположения осей ведущего и ведомого валов, в частности, межосевого расстояния a_w ;

– малые потери при передаче мощности (высокий кпд) и, как следствие, ограниченный нагрев и износ;

– плавная и бесшумная работа;

– прочность, долговечность, надёжность.

Передачи имеют широкое распространение в машиностроении по следующим причинам:

1) энергию целесообразно передавать при больших частотах вращения;

2) требуемые скорости движения рабочих органов машин, как правило, не совпадают с оптимальными скоростями двигателя; обычно ниже, а создание тихоходных двигателей вызывает увеличение габаритов и стоимости;

3) скорость исполнительного органа в процессе работы машины-орудия необходимо изменять (например, у автомобиля, грузоподъемного крана, токарного станка), а скорость машины-двигателя чаще посто­янна (например, у электродвигателей);

4) нередко от одного двигателя необходимо приводить в движение не­сколько механизмов с различными скоростями;

5) в отдельные периоды работы исполнительному органу машины тре­буется передать вращающие моменты, превышающие моменты на валу машины-двигателя, а это возможно выполнить за счет уменьше­ния угловой скорости вала машины-орудия;

6) двигатели обычно выполняют для равномерного вращательного движения, а в машинах часто оказывается необходимым поступательное движение с определенным законом;

7) двигатели не всегда могут быть непосредственно соединены с исполнительными механизмами из-за габаритов машины, условий техники безопасности и удобства обслуживания;

8) распределять работу двигателя между несколькими исполнительными органами машины.

Как правило, угловые скорости валов большинства используемых в настоящее время в технике двигателей (поршневых двигателей внутреннего сгорания, газотурбинных, электрических, гидравлических и пневматических двигателей) значительно превышают угловые скорости валов исполнительных или рабочих органов машин, порой на 2-3 порядка. Поэтому доставка (передача) энергии двигателя с помощью передачи любого типа, в том числе и механической, происходит, как правило, совместно с одновременным преобразованием моментов и угловых скоростей (в сторону повышения первых и понижения последних).

При этом необходимо отметить, что конструктивное обеспечение функции транспортного характера – чисто передачи энергии иной раз вступает в логическое противоречие с направлением задачи конечного преобразования силовых и скоростных параметров этой энергии. Например, в трансмиссиях многих транспортных машин (особенно высокой проходимости) входной редуктор сначала повышает частоту вращения, понижение ее до требуемых пределов производят бортовые или колесные редукторы.

Этот прием позволяет снизить габаритно-весовые показатели промежуточных элементов трансмиссии (коробок перемены передач, карданных валов) – размеры валов и шестерен пропорциональны величине передаваемого крутящего момента в степени 1/3.

Аналогичный принцип используется при передаче электроэнергии – повышение напряжения перед ЛЭП позволяет значительно снизить тепловые потери, определяемые в основном силой тока в проводах, а заодно уменьшить сечение этих проводов.

Иногда передача механической энергии двигателя сопровождается также преобразованием вида движения (например, поступательного движения во вращательное или наоборот) или законов движения (например, равномерного движения в неравномерное).

Широко известными образцами таких передач являются кривошипно-шатунный механизм и кулачковый привод механизма газораспределения.

Классификация механических передач

Механические передачи, применяемые в машиностроении, класси­фицируют (рис.1 и 2):

по энергетической характеристике механические передачи делятся на :

– кинематические (передаваемая мощность Р -1 ), и передаточным отношением u .

Это три основные характеристики, необходимые для проектировочного расчета любой передачи.

Рис. 3. Основные параметры передач

Рис. 4. Трехступенчатая передача

Рис. 5. Кинематика ци­линдрической передачи

В машиностроении принято обозначать угловые и окружные скорости, частоту вращения, диаметры вращающихся деталей ведущих валов индексами нечетных цифр, ведомых — четными. Например, для колес трехступенчатой передачи (рис. 4) обо­значения частот вращения следующие: п ₁ — веду­щего вала I ; п₃ — ведущей шестерни вала II ; п₅ — ведущей шестерни вала III ; п₂ — промежуточного ведомого вала II ; п₄ — ведомого колеса вала III ; п₆ — ведомого колеса вала IV .

Все механические передачи характеризуются передаточным числом или отношением. Рассмотрим работу двух элементов передачи (рис.5), один из которых будет ведущим, а второй — ведомым.

Введем следующие обозначения: ω ₁ и п ₁ — угло­вая скорость и частота вращения ведущего вала, выраженные соответственно рад/с и об/мин; ω ₂ и п₂ — угловая скорость и частота вращения ведомого вала; D ₁ и D ₂ – диаметры вращающихся деталей (шкивов, катков и т. п.); ν ₁ и ν ₂ — окружные скоро­сти, м/с.

Передаточное число – отношение угловой скорости ве­дущего вала к угловой скорости ведомого вала конкретной передачи. Передаточное число не может быть меньше единицы . Оно представляет собой абсолютную величину передаточного отношения:

Принимая в точке контакта

Диаметр начальных окружностей зубчатых колес зубчатой передачи определяется по формулам:

Таким образом, для любой передачи:

Отношение угловых скоростей ведущего ω ₁ и ведомого ω ₂ звеньев называют также передаточным отношением и обозначают і .

Передаточное число в отличие от передаточного отношения всегда положительное и не может быть меньше единицы. Передаточное число характеризует передачу только количественно. Передаточное число и передаточное отношение могут совпадать только у передачи внутреннего зацепления. У передач внешнего зацепления они не совпадают, так как имеют разные знаки: передаточное отношение – отрицательное, а передаточное число – положительное. Если ведущее и ведомое колеса вращаются в одну сторону (например, у зубчатой передачи с внутренним зацеплением), то передаточное отношение считается положительным. Если ведомое и ведущее колеса вращаются в разные стороны (например, у зубчатой передачи внешнего зацепления), то передаточное отношение считается отрицательным.

В передаче, понижающей частоту вращения n (угловую скорость ω ), u >1; при и Р₂.

Отношение значений мощности на ведомом валу P ₂ к мощности на веду­щем валу P ₁ называют механическим коэффициентом полезного действия (КПД) и обозначают буквой η :

Общий КПД многоступенчатой последовательно соединенной переда­чи определяют по формуле

где 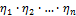— КПД, учитывающие потери в отдельных кинематических парах передачи (подшипники, муфты).

Следовательно КПД машины, содержащей ряд последовательных передач, всегда будет меньше КПД любой из этих передач.

КПД характеризует качество передачи. Потеря мощности – показатель непроизводительных затрат энергии – косвенно характеризует износ деталей передачи, так как потерянная в передаче мощность превращается в теплоту и частично идет на разрушение рабочих поверхностей.

С уменьшением полезной нагрузки КПД значительно снижается, так как возрастает относительное влияние постоянных потерь (близких к потерям холостого хода), не зависящих от нагрузки.

Отношение потерянной в механизме (машине) мощности ( P ₁ – P ₂) к ее входной мощности называют коэффициентом потерь, который можно выразить следующим образом:

Следовательно сумма коэффициентов полезного действия и потерь всегда равна единице:

Окружная скорость ведущего или ведомого звена, м/ с ,

где ω – угловая скорость ,с -1 ; n – частота вращения, мин –1 ; d – диаметр, мм (колеса, шкива и др.)

Окружные скорости обоих звеньев передачи при отсутствии скольжения равны: ;

Окружная сила, Н,

где Р –м ощность, кВт; ν – м/с; Т– Нм ; d – мм;

Вращающий (крутящий) момент, Нм ,

Вращающий момент Т ₁ ведущего вала является моментом движущих сил, его направление совпадает с направлением вращения вала. Момент Т ₂ ведомого вала – момент сил сопротивления поэтому его направление противоположно направлению вращения вала;

Передачи с постоянным передаточным числом

В задании на проектирование с постоянным передаточным числом должны быть известны: передаваемая мощность N или крутящий момент T на ведомом валу, частота вращения ведущего n ₁ и ведомого n ₂ валов, схема передачи, габариты и режим работы передачи.

По этим данным можно спроектировать несколько передач различных типов. Возможные варианты передач нужно сравнить между собой по весу, КПД, габаритам и др. параметрам и выбрать из них наивыгоднейший . В таблице 2 приводятся некоторые параметры различных передач.

Таблица 2. Ориентировочные знания основных параметров одноступенчатых механических передач

Фрикционная передача

В случае фрикционной передачи два колеса прижаты друг к другу с некоторой силой. При вращении одного колеса, например, по часовой стрелке другое колесо благодаря трению приходит тоже во вращение и движется против часовой стрелки. Такая передача имеется, например, в швейной машине между колесом и шпулькомоталкой, между тахометром и валом двигателя при измерении числа оборотов.

Вообще фрикционная передача применяется при небольших мощностях. Как известно, при одной и той же скорости мощность пропорциональна величине действующей силы. Сила же, действующая на ведомое фрикционное колесо, зависит от силы трения между обоими колёсами. Но сила трения зависит от силы давления.

Следовательно, при большой мощности оба колеса должны быть прижаты друг к другу с очень большой силой, вследствие чего вал, на котором насажено колесо, может изогнуться.

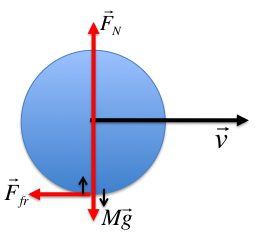
Силы, действующие на твёрдое тело, вращающееся вокруг оси

Проделаем следующий опыт. Намотаем на диск нить и потянем её. На диск будут действовать две разные силы:

сила натяжения нити и сила трения диска о стол. Под действием этих сил диск будет вращаться и одновременно перемещаться.

Если же намотать на диск две нити так, и потянуть за нити в противоположные стороны, приложив равные силы, то диск будет только вращаться.

Две равные, параллельные и противоположно направленные силы называются парой сил.

Зубчатая передача

Передача зубчатыми колёсами, или шестернями, находит самое широкое применение в технике. Так, при помощи зубчатых колёс осуществляется передача от двигателя к ведущим колёсам в автомобиле, тракторе и трамвае. При помощи зубчатых колёс передаётся движение от двигателя к гребному винту парохода. Зубчатые колёса применяются во многих станках для передачи движения от двигателя к станку и т. д. На рисунке изображено применение зубчатых колёс в ручной лебёдке.

С помощью шестерён можно вращательное движение преобразовать в поступательное, как это показано на рисунке. На этом рисунке изображена упрощённая схема одного из наиболее употребительных механизмов строгального станка. Движение от шкива D (который приводится во вращение ремнём) передаётся при помощи валов и системы шестерён, сидящих на этих валах, зубчатой рейке R. Зубчатая рейка движется поступательно в направлении, указанном на рисунке оперённой стрелкой. Вместе с ней движется и стол станка (не изображён на рисунке), с которым скреплена рейка. Когда рейка дойдёт до конца, особым приспособлением перекрещённый ремень переводится на шкив D₁. Рейка при этом получит обратный ход (холостой) в направлении, обозначенном простой стрелкой.

Число оборотов ведомого колеса зависит от числа оборотов ведущего и числа зубьев на обоих колёсах.

Пусть одна шестерня имеет z₁ зубьев и делает n₁ оборотов в секунду, другая же, сцепленная с ней шестерня имеет z₂ зубьев и делает n₂ оборотов.

У первой шестерни за 1 секунду через точку сцепления пройдёт z₁n₁ зубьев, а у второй шестерни – z₂n₂. Так как числа прошедших зубьев на обеих шестернях равны, то

Ремённая передача

При ремённой передаче два колеса–шкива, укреплённые на разных валах, охватываются «бесконечным» приводным ремнём. Шкив А на валу двигателя называется ведущим, а шкив В на валу станка – ведомым. Если диаметры шкивов неодинаковы, то, так как скорости на окружностях того и другого шкива при отсутствии скольжения равны, числа их оборотов будут различны.

Пусть D₁ –диаметр ведущего шкива и он делает n₁ оборотов в секунду, a D₂ – диаметр ведомого шкива и n₂ – число его оборотов, v – скорость на окружностях обоих шкивов.

v = ?D₁n и v = ?D₂n₂

Разделив равенство (2) на (1), получим:

Числа оборотов шкивов в единицу времени обратно пропорциональны диаметрам шкивов. Отношение n₂/n₁ называется передаточным числом.

Из равенства (3) следует, что число оборотов вала станка тем больше, чем меньше диаметр его шкива.

Вращательное движение твердых тел

Простейшие движения твёрдого тела – поступательное и вращательное. С поступательным движением мы уже ознакомились в первой части курса.

Вращательное движение твёрдых тел весьма распространено в природе и технике. Например: движение Земли вокруг своей оси, движение шкивов, маховых колёс и обтачиваемых на токарных станках деталей, движение граммофонной пластинки и т. п.

На рисунке стрелками показано вращательное движение детали на токарном станке и поступательное движение резца.

Любое движение твёрдого тела может быть представлено как результат поступательного и вращательного движений. Особенно хорошо это видно на примере винтового движения. Болт, например, ввинчиваясь в гайку, движется поступательно и одновременно вращается. Сверло при работе также одновременно вращается и движется поступательно. Колесо повозки, вращаясь вокруг оси, одновременно вместе с повозкой движется поступательно. Таких примеров можно привести сколько угодно.

Возьмём картонный диск с нарисованными на нём кружочками на разных расстояниях от центра и приведём его в быстрое вращение – мы увидим ряд окружностей разных радиусов. Этот опыт показывает, что при вращательном движении тела различные его точки движутся по окружностям; центры этих окружностей лежат на прямой, называемой осью вращения. Угол поворота радиусов окружностей за данный промежуток времени для всех точек тела одинаков. Поэтому углом поворота радиуса окружности одной какой-нибудь точки тела за данный промежуток времени можно характеризовать движение всех точек тела, т. е. вращение тела в целом. Но угол поворота в 1 сек численно равен угловой скорости. Следовательно, угловая скорость у всех точек вращающегося тела одна и та же.

Передача вращения от двигателя к машине-орудию

Машины разделяются на двигатели и машины–орудия. Двигатели – это, например, паровая машина, паровая турбина, гидротурбина, электродвигатель и др. К машинам–орудиям относятся станки и машины, вырабатывающие различного рода изделия, например: токарный станок, ткацкий станок, прядильная машина и др.

Для работы станка необходимо, чтобы вращение от вала двигателя передавалось на вал станка. Такая передача движения осуществляется различными способами. Чаще всего для этого применяются следующие три способа передачи: ремённая, фрикционная и зубчатая.

Передачи вращательного движения

Общие сведения о механических передачах

Для приведения в движение рабочих машин механическая энергия им передается от машин-двигателей (двигателей внутреннего сгорания, электродвигателей и т.п.). Как правило, двигатели и исполнительные органы рабочих машин связываются между собой при помощи механизмов, называемых передачами. Передачи бывают механические, гидравлические, пневматические и электрические. В лесном хозяйстве основное применение нашли механические передачи. Наибольшее распространение в механических передачах нашло вращательное движение. Механизм, предназначенный для передачи энергии от двигателя к её потребителям с увеличением крутящего момента за счёт уменьшения частоты вращения, называется силовой передачей или трансмиссией.

Механические передачи классифицируются по следующим признакам:

• – по способу передачи движения: трением – фрикционные, ремённые; зацеплением зубчатые, червячные, цепные, винт-гайка.
• – по способу соединения звеньев: с непосредственным контактом – фрикционные, зубчатые, червячные, винт-гайка; с гибкой связью – ремённые, цепные.

Звено передачи, получающее движение от двигателя, называется ведущим; звено, которому передаётся движение, называется ведомым. Между ведущим и ведомым звеньями могут располагаться промежуточные звенья.

На рис. 93,а показана схема передачи с гибкой связью, а на рис. 93,6 – передача с непосредственным контактом. На схемах индексом 1 обозначены ведущие звенья и параметры, относящиеся к ним; индексом 2 – ведомые звенья и их параметры. Следует отметить, что при гибкой связи направление вращения ведущего и ведомого звена совпадает, а при передаче с непосредственным контактом – изменяется на противоположное. В этом случае для совпадения направления вращения между ведущим и ведомым звеном устанавливается промежуточное звено.

Рис. 93. Механические передачи: а – гибкой связью; б – с непосредственным контактом

Основными параметрами вращательных передач являются передаточное число, передаваемая мощность и КПД.

Передаточным отношением называется отношение угловой скорости ведущего звена к угловой скорости ведомого звена. Оно может быть больше, меньше или равно единице.

Передаточным числом называется отношение большей угловой скорости к меньшей. Передаточное число не может быть меньше единицы.

Для унификации передаточные отношения и передаточные числа всех передач обозначаются буквой и и при необходимости с двойным индексом, соответствующим ведущему и ведомому звеньям. Так, передаточное отношение одноступенчатой передачи будет

где ©1 и ©2 – угловая скорость соответственно ведущего и ведомого звеньев;

п и п₂ – частота вращения ведущего и ведомого звеньев.

Однако следует отметить, что в расчётные формулы на прочность деталей машин всегда входят передаточные числа, то есть и ? 1.

Передачи, у которых угловая скорость ведомого звена меньше угловой скорости ведущего, то есть ©i > ©2, называются понижающими; в противном случае, когда ©i

Источники:

http://pfaves.ru/stati/mehanizmy-peredachi-dvizheniya-ispolzuemye-v-tokarnyh-stankah
http://www.syl.ru/article/189925/new_vraschatelnoe-dvijenie-tela-zakon-vraschatelnogo-dvijeniya
http://www.sites.google.com/site/tehmehprimizt/lekcii/detali-masin/peredaci-vrasatelnogo-dvizenia
http://scibio.ru/fizika/mekhanika/vrashchatelnoe_dvizhenie.html
http://studme.org/187811/tehnika/peredachi_vraschatelnogo_dvizheniya